\(\newcommand{\AA}{\unicode{x212B}}\)
14.5. XAFS: Fourier Transforms for XAFS¶
Fourier transforms are central to understanding and using
XAFS. Consequently, many of the XAFS functions in Larch use XAFS Fourier
transforms as part of their processing, and many of the functions
parameters and arguments described here have names and meanings used
throughout the XAFS functionality of Larch. For example, both
autobk() and feffit() rely on XAFS Fourier transforms, and use
the XAFS Fourier transform function described here.
14.5.1. Overview of XAFS Fourier transforms¶
The standard Fourier transform of a signal \(f(t)\) can be written as
where the symmetric normalization is one of the more common choices of conventions. This gives conjugate variables of \(\omega\) and \(t\). Because XAFS goes as
the conjugate variables in XAFS are generally taken to be \(k\) and \(2R\). The normalization of \(\tilde\chi(R)\) from a Fourier transform of \(\chi(k)\) is a matter of convention, but we follow the symmetric case above (with \(t\) replaced by \(k\) and \(\omega\) replaced by \(2R\), and of course \(f\) by \(\chi\)).
But there are two more important issues to mention. First, an XAFS Fourier transform multiplies \(\chi(k)\) by a power of \(k\), \(k^n\) and by a window function \(\Omega(k)\) before doing the Fourier transform. The power-law weighting allow the oscillations in \(k\) to emphasize different portions of the spectra, or to give a uniform intensity to the oscillations. The window function acts to smooth the resulting Fourier transform and remove ripple and ringing in it that would result from a sudden truncation of \(\chi(k)\) at the end of the data range.
The second important issue is that the continuous Fourier transform
described above is replaced by a discrete transform. This better matches
the discrete sampling of energy and \(k\) values of the data, and
allows Fast Fourier Transform techniques to be used. It does change the
definitions of the transforms used somewhat. First, the \(\chi(k)\)
data must be on uniformly spaced set of \(k\) values. The default
\(k\) spacing used in Larch (including as output from autobk())
is \(\delta k\) = 0.05 \(\rm\AA^{-1}\). Second, the array size for
\(\chi(k)\) used in the Fourier transform should be a power of 2. The
default used in Larch is \(N_{\rm fft}\) = 2048. Together, these
allow \(\chi(k)\) data to 102.4 \(\rm\AA^{-1}\). Of course, real
data doesn’t extend that far, so the array to be transformed is
zero-padded to the end of the range. Since the spacing \(\delta R\)
of the resulting discrete \(\chi(R)\) is given as
\(\pi/{(N_{\rm fft} \delta k )}\), the extended range and zero-padding
will increase the density of points in \(\chi(R)\), smoothly
interpolating the values. For \(N_{\rm fft}\) = 2048 and
\(\delta k\) = 0.05 \(\rm\AA^{-1}\), the \(R\) spacing is
approximately \(\delta R\) = 0.0307 \(\rm\AA\).
For the discrete Fourier transforms with samples of \(\chi(k)\) at the points \(k_n = n \, \delta k\), and samples of \(\chi(R)\) at the points \(R_m = m \, \delta R\), the definitions become:
These normalizations preserve the symmetry properties of the Fourier Transforms with conjugate variables \(k\) and \(2R\). Though the reverse transform converts the complex \(\chi(R)\) to the complex \(\chi(k)\) on the same \(k\) spacing as the starting data, we often refer to the filtered \(\chi(k)\) as q space.
A final complication in using Fourier transforms for XAFS is that the measured \(\mu(E)\) and \(\chi(k)\) are a strictly real values, while the Fourier transform inherently treats \(\chi(k)\) and \(\chi(R)\) as complex values. This leads to an ambiguity about how to construct the complex \(\tilde\chi(k)\). In many formal treatments, XAFS is written as the imaginary part of a complex function. This might lead one to assume that constructing \(\tilde\chi(k)\) as \(0 + i\chi(k)\) would be the natural choice. For historical reasons, Larch uses the opposite convention, constructing \(\tilde\chi(k)\) as \(\chi(k) + 0i\). As we’ll see below, you can easily change this convention. The effect of this choice is minor unless one is concerned about the differences of the real and imaginary parts of \(\chi(R)\) or one is intending to filter and back-transform the \(\chi(R)\) and compare the filtered and unfiltered data.
14.5.2. Forward XAFS Fourier transforms (\(k{\rightarrow}R\))¶
The forward Fourier transform converts \(\chi(k)\) to \(\chi(R)\)
and is of primary importance for XAFS analysis. In Larch, this is
encapsulated in the xftf() function.
- xftf(k, chi=None, group=None, ...)¶
perform a forward XAFS Fourier transform, from \(\chi(k)\) to \(\chi(R)\), using common XAFS conventions.
- Parameters:
k – 1-d array of photo-electron wavenumber in \(\rm\AA^{-1}\)
chi – 1-d array of \(\chi\)
group – output Group
rmax_out – highest R for output data (10 \(\rm\AA\))
kweight – exponent for weighting spectra by \(k^{\rm kweight}\)
kmin – starting k for FT Window
kmax – ending k for FT Window
dk – tapering parameter for FT Window
dk2 – second tapering parameter for FT Window
window – name of window type
nfft – value to use for \(N_{\rm fft}\) (2048).
kstep – value to use for \(\delta{k}\) (0.05).
- Returns:
None– outputs are written to supplied group.
Follows the First Argument Group convention, using group members named
kandchi. The following data is put into the output group:array name
meaning
kwin
window \(\Omega(k)\) (length of input chi(k)).
r
uniform array of \(R\), out to
rmax_out.chir
complex array of \(\tilde\chi(R)\).
chir_mag
magnitude of \(\tilde\chi(R)\).
chir_pha
phase of \(\tilde\chi(R)\).
chir_re
real part of \(\tilde\chi(R)\).
chir_im
imaginary part of \(\tilde\chi(R)\).
It is expected that the input
kbe a uniformly spaced array of values with spacingkstep, starting a 0. If it is not, thekandchidata will be linearly interpolated onto the proper grid.The FT window parameters are explained in more detail in the discussion of
ftwindow().
- xftf_fast(chi, nfft=2048, kstep=0.05)¶
perform a forward XAFS Fourier transform, from \(\chi(k)\) to \(\chi(R)\), using common XAFS conventions. This version demands
chito include any weighting and windowing, and so to represent \(\chi(k)k^w\Omega(k)\) on a uniform \(k\) grid. It returns the complex array of \(\chi(R)\).- Parameters:
chi – 1-d array of \(\chi\) to be transformed
nfft – value to use for \(N_{\rm fft}\) (2048).
kstep – value to use for \(\delta{k}\) (0.05).
- Returns:
complex \(\chi(R)\).
14.5.3. Reverse XAFS Fourier transforms (\(R{\rightarrow}q\))¶
Reverse Fourier transforms convert \(\chi(R)\) back to filtered \(\chi(k)\). We refer to the filtered \(k\) space as \(q\) to emphasize the distinction between the two. The filtered \(\chi(q)\) is complex. By convention, the real part of \(\chi(q)\) corresponds to the explicitly real \(\chi(k)\).
- xftr(r, chir, group=None, ...)¶
perform a reverse XAFS Fourier transform, from \(\chi(R)\) to \(\chi(q)\).
- Parameters:
r – 1-d array of distance.
chir – 1-d array of \(\chi(R)\)
group – output Group
qmax_out – highest k for output data (30 \(\rm\AA^{-1}\))
rweight – exponent for weighting spectra by \(r^{\rm rweight}\) (0)
rmin – starting R for FT Window
rmax – ending R for FT Window
dr – tapering parameter for FT Window
dr2 – second tapering parameter for FT Window
window – name of window type
nfft – value to use for \(N_{\rm fft}\) (2048).
kstep – value to use for \(\delta{k}\) (0.05).
- Returns:
None– outputs are written to supplied group.
Follows the First Argument Group convention, using group members named
randchir. The following data is put into the output group:array name
meaning
rwin
window \(\Omega(R)\) (length of input chi(R)).
q
uniform array of \(k\), out to
qmax_out.chiq
complex array of \(\tilde\chi(k)\).
chiq_mag
magnitude of \(\tilde\chi(k)\).
chiq_pha
phase of \(\tilde\chi(k)\).
chiq_re
real part of \(\tilde\chi(k)\).
chiq_im
imaginary part of \(\tilde\chi(k)\).
In analogy with
xftf(), it is expected that the inputrbe a uniformly spaced array of values starting a 0.The input
chirarray can be either the complex \(\chi(R)\) array as output toGroup.chirfromxftf(), or one of the real or imaginary parts of the \(\chi(R)\) as output toGroup.chir_reorGroup.chir_im.The FT window parameters are explained in more detail in the discussion of
ftwindow().
- xftr_fast(chir, nfft=2048, kstep=0.05)¶
perform a reverse XAFS Fourier transform, from \(\chi(R)\) to \(\chi(q)\), using common XAFS conventions. This version demands
chirbe the complex \(\chi(R)\) as created fromxftf(). It returns the complex array of \(\chi(q)\) without putting any values into a group.- Parameters:
chir – 1-d array of \(\chi(R)\) to be transformed
nfft – value to use for \(N_{\rm fft}\) (2048).
kstep – value to use for \(\delta{k}\) (0.05).
- Returns:
complex \(\chi(q)\).
14.5.4. ftwindow(): Generating Fourier transform windows¶
As mentioned above, a Fourier transform window will smooth the resulting Fourier transformed spectrum, removing ripple and ringing in it that would result from a sudden truncation data at the end of it range. There is an extensive literature on such windows, and a lot of choices and parameters available for constructing windows. A sampling of windows is shown below.
- ftwindow(x, xmin=0, xmax=None, dk=1, ...)¶
create a Fourier transform window array.
- Parameters:
x – 1-d array array to build window on.
xmin – starting x for FT Window
xmax – ending x for FT Window
dx – tapering parameter for FT Window
dx2 – second tapering parameter for FT Window (=dx)
window – name of window type
- Returns:
1-d window array.
Note that if
dxis specified butdx2is not,dx2will generally take the same value asdx.The window type must be one of those listed in the Table of Fourier Transform Window Types.
Table of Fourier Transform Window Types.
window name
description
hanning
cosine-squared taper
parzen
linear taper
welch
quadratic taper
gaussian
Gaussian (normal) function window
sine
sine function window
kaiser
Kaiser-Bessel function-derived window
In general, the window arrays have a value that gradually increases from 0
up to 1 at the low-k end, may stay with a value 1 over some central
portion, and then tapers down to 0 at the high-k end. The meaning of the
dx and dx2, and even xmin, and xmax varies a bit for the
different window types. The Hanning, Parzen, and Welch windows share a
convention that the windows taper up from 0 to 1 between xmin-dx/2 and
xmin+dx/2, and then taper down from 1 to 0 between xmax-dx2/2 and
xmax+dx2/2.
The conventions for the Kaiser, Gaussian, and Sine window types is a bit
more complicated, and is best given explicitly. In the formulas below,
dx written as \(dx\) and dx2 as \(dx_2\). We
define \(x_i = x_{\rm min} - dx/2\), \(x_f = x_{\rm max} +
dx_2/2\), and \(x_0 = (x_f + x_i)/2\), as the beginning, end, and
center of the widows. For the Gaussian window, the form is:
The form for the Sine window is
between \(x_i\) and \(x_f\), and 0 outside this range. The Kaiser-Bessel window is slightly more complicated:
where \(i_0\) is the modified Bessel function of order 0.
14.5.5. Catalog of Fourier transform window¶
Here, we give a series of example windows, to illustrate the different
window types and the effect of the various parameters. The meanings of
xmin, xmax, dx and dx2 are identical for the Hanning, Parzen and
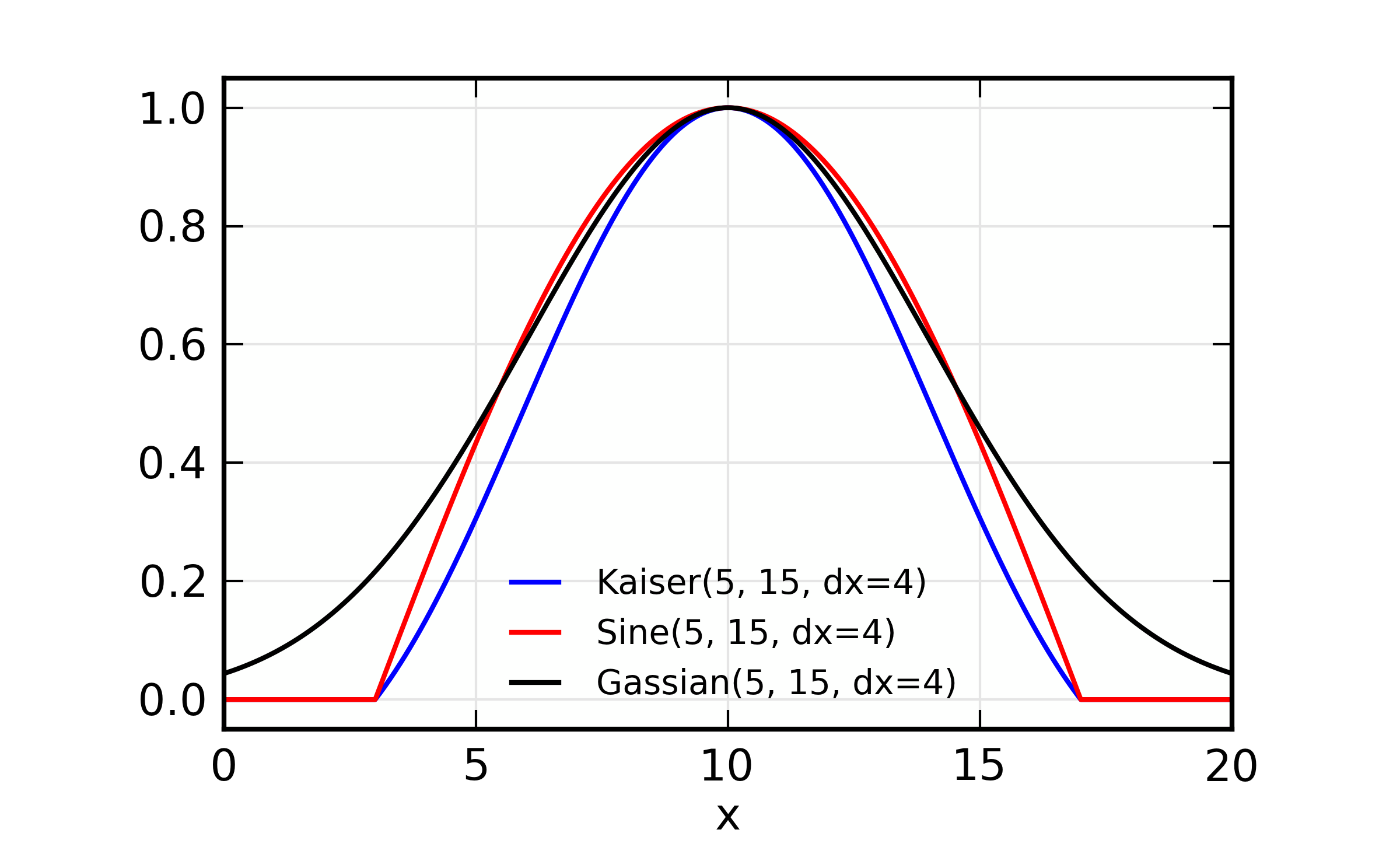
Welch windows, and illustrated in the two following figures.
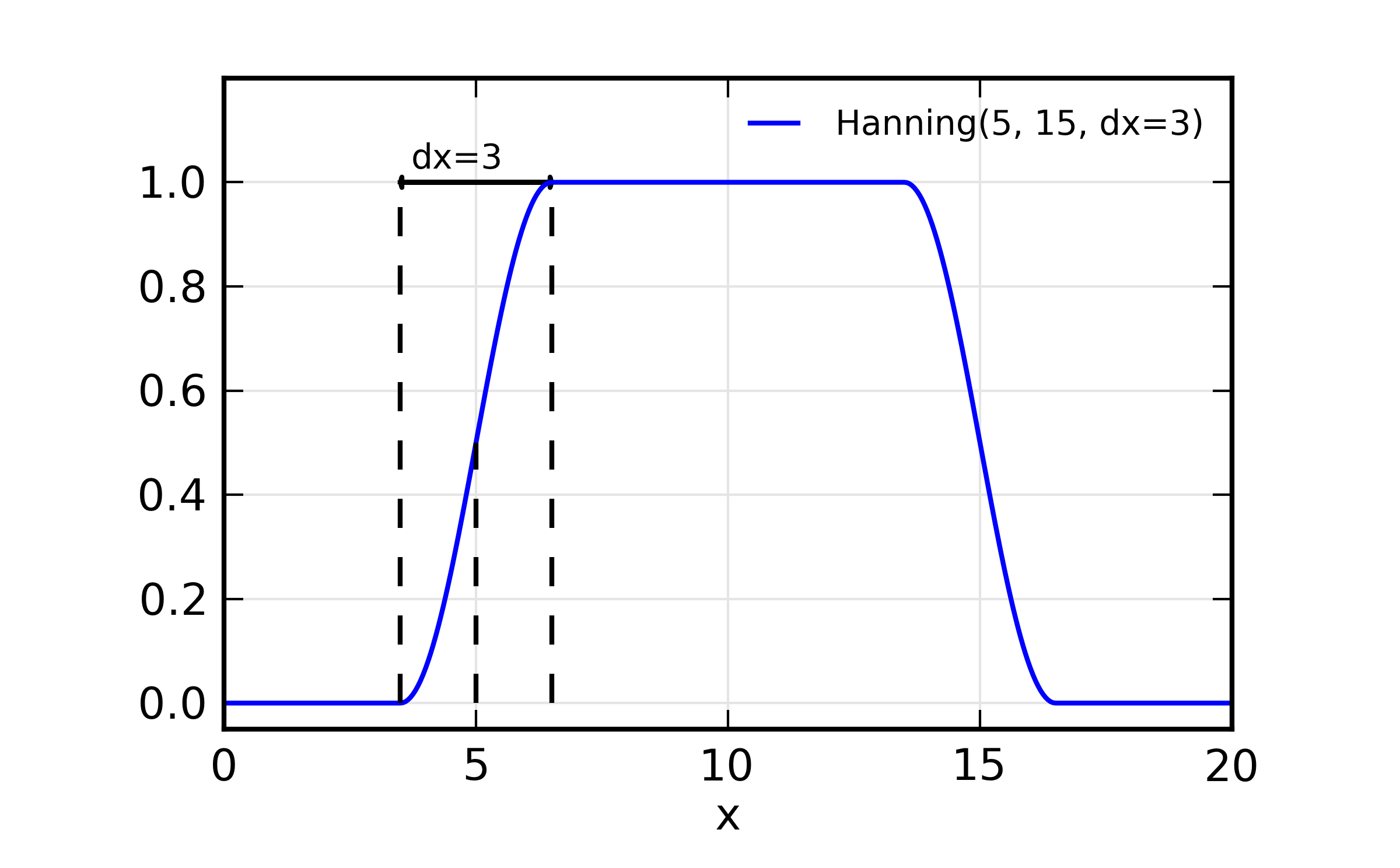

Fourier Transform window examples and illustration of parameter meaning
for the Hanning, Parzen, and Welch windows. Note that
\(\Omega(x=x_{\rm min}) = \Omega(x=x_{\rm max}) = 0.5\), and that
the meaning of dx is to control the taper over which the window
changes from 0 to 1. Here, xmin=5 and xmax=15.
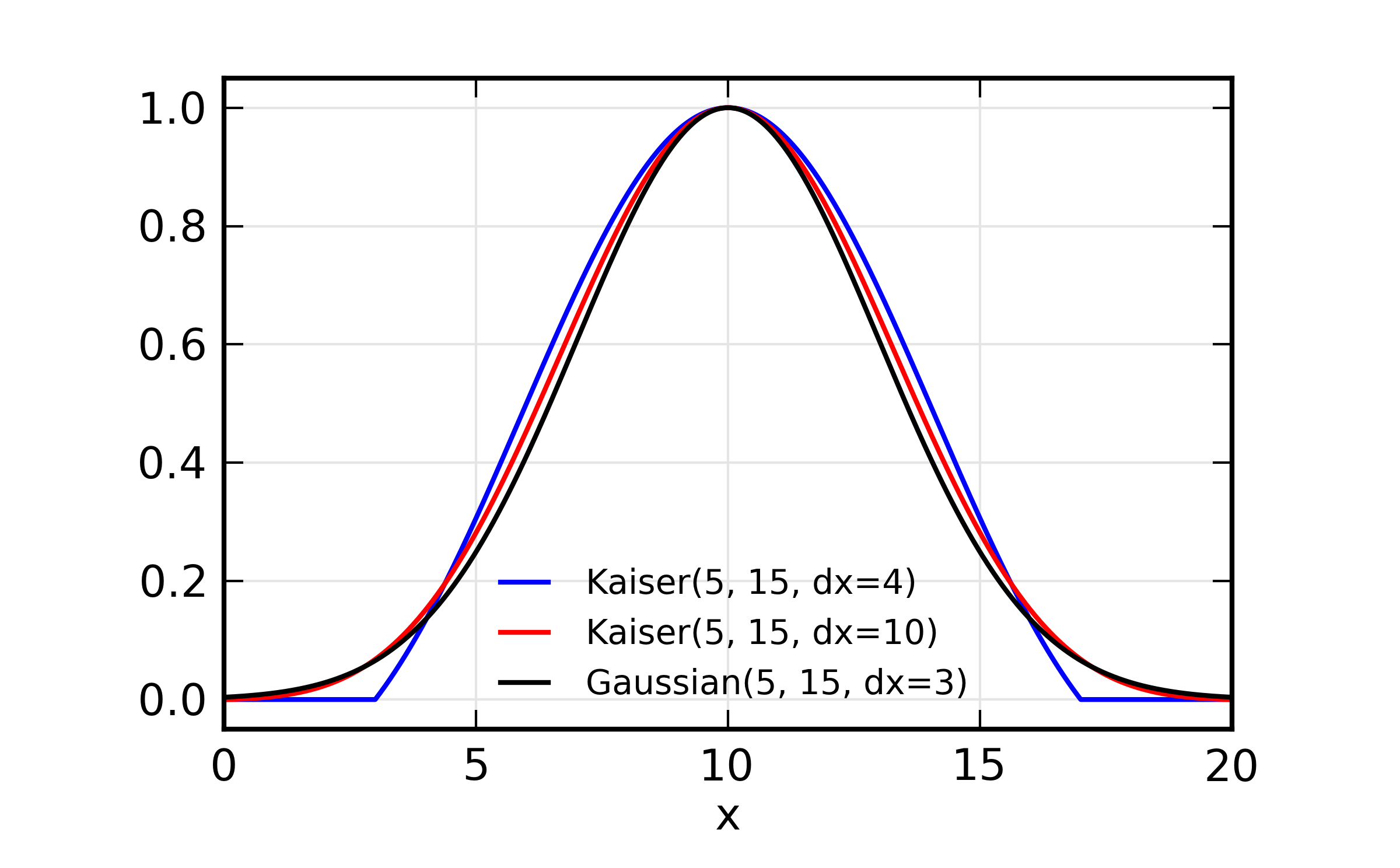
Some more window functions:

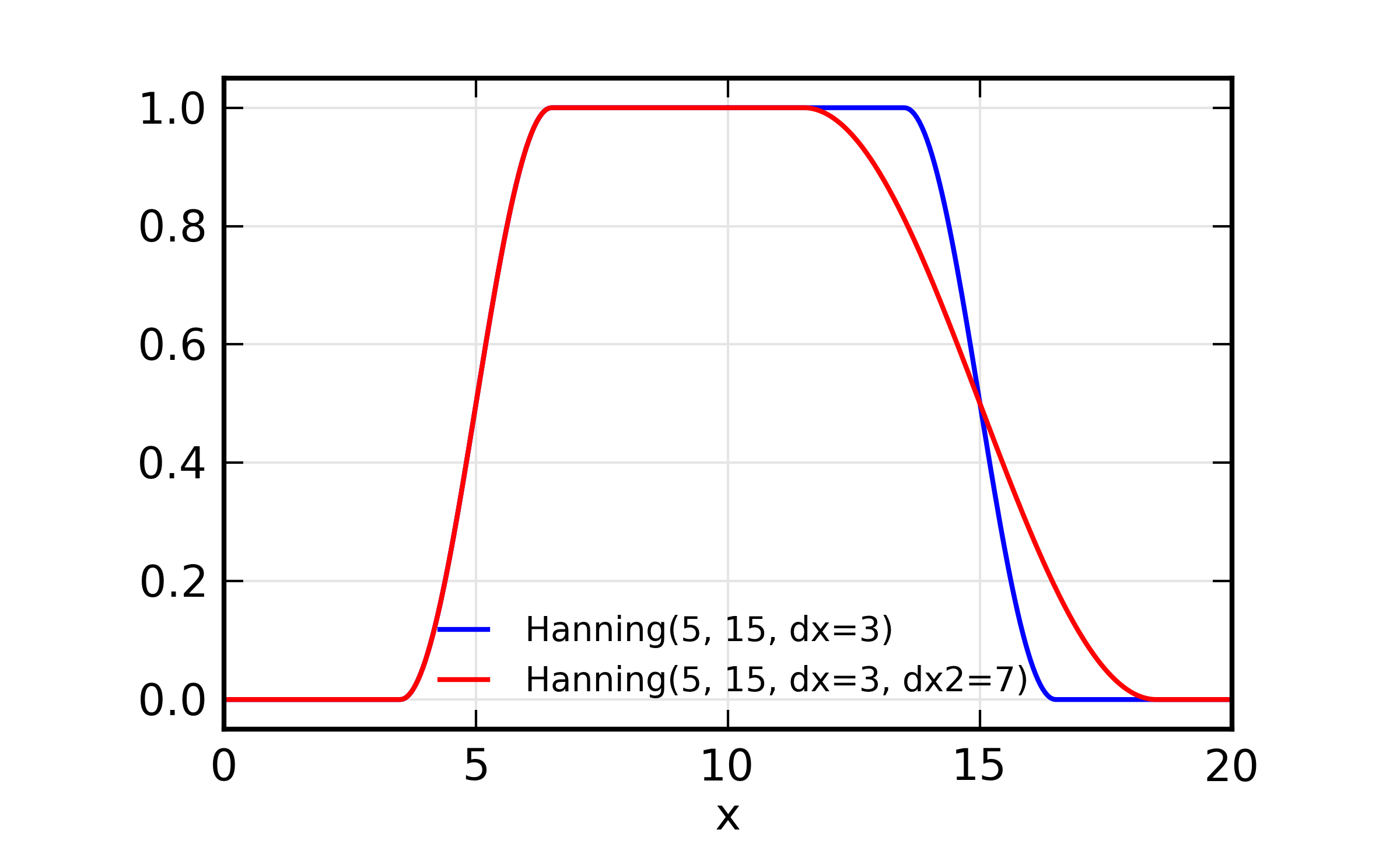
Fourier Transform window examples and illustration of parameter
meaning. On the left, a comparison of Welch, Parzen, and Hanning with
the same parameters is shown. On the right, the effect of dx2 is
shown as a different amount of taper on the high- and low-x end of
the window. As before, xmin=5 and xmax=15.
The Gaussian, Sine, and Kaiser-Bessel windows are illustrated next. These
go to 1 at the average of xmin and xmax, but do not stay at 1 over
a central portion of the window – they taper continuously. The Gaussian
window is a simple Gaussian function, and is not truncated according to
xmin and xmax, and the dx parameter sets the width. The Sine
and Kaiser-Bessel windows both go to zero at xmin-dx/2 and xmax +
dx/2. For very large values of dx, the Kaiser-Bessel window
approaches a nearly Gaussian lineshape.
14.5.6. Examples: Forward XAFS Fourier transforms¶
Now we show some example Fourier transforms, illustrating the real and imaginary parts of the \(\chi(R)\) as well as the magnitude, the effect of different windows types, and Fourier filtering to \(\chi(q)\). We use a single XAFS dataset from FeO for all these examples, with a well-separated first and second shell. The full scripts to generate the figures shown here are included in the examples/xafs/ folder.
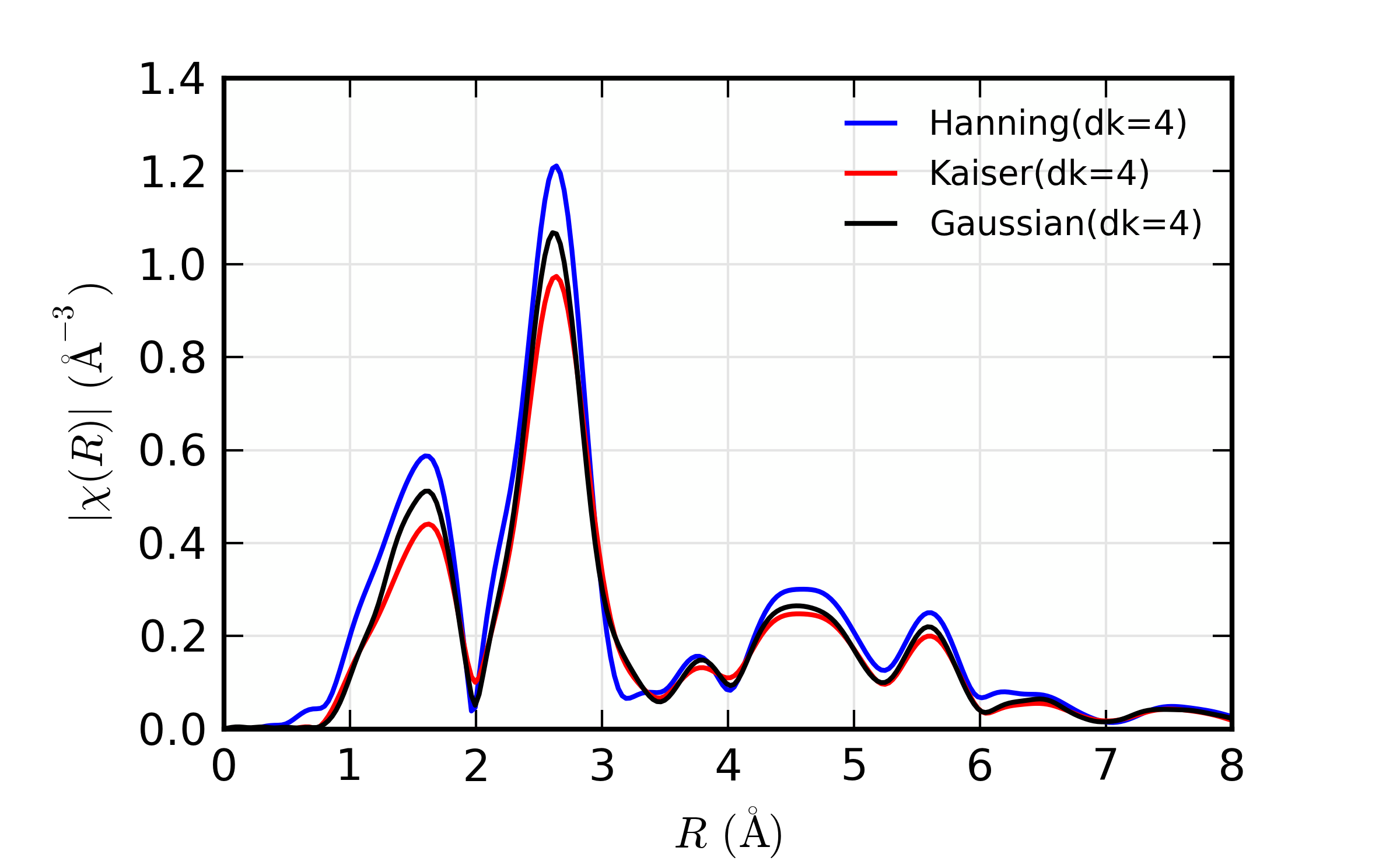
We start with a comparison of a small value of dk and a larger value.
A script that runs xftf(), changing on dk would look like:
xftf(dat1.k, dat1.chi, kmin=3, kmax=13, dk=1, window='hanning',
kweight=kweight, group=dat1)
dat2 = group(k=dat1.k, chi=dat1.chi) # make a copy of the group
xftf(dat2.k, dat2.chi, kmin=3, kmax=13, dk=5, window='hanning',
kweight=kweight, group=dat2)
would result in the following results:
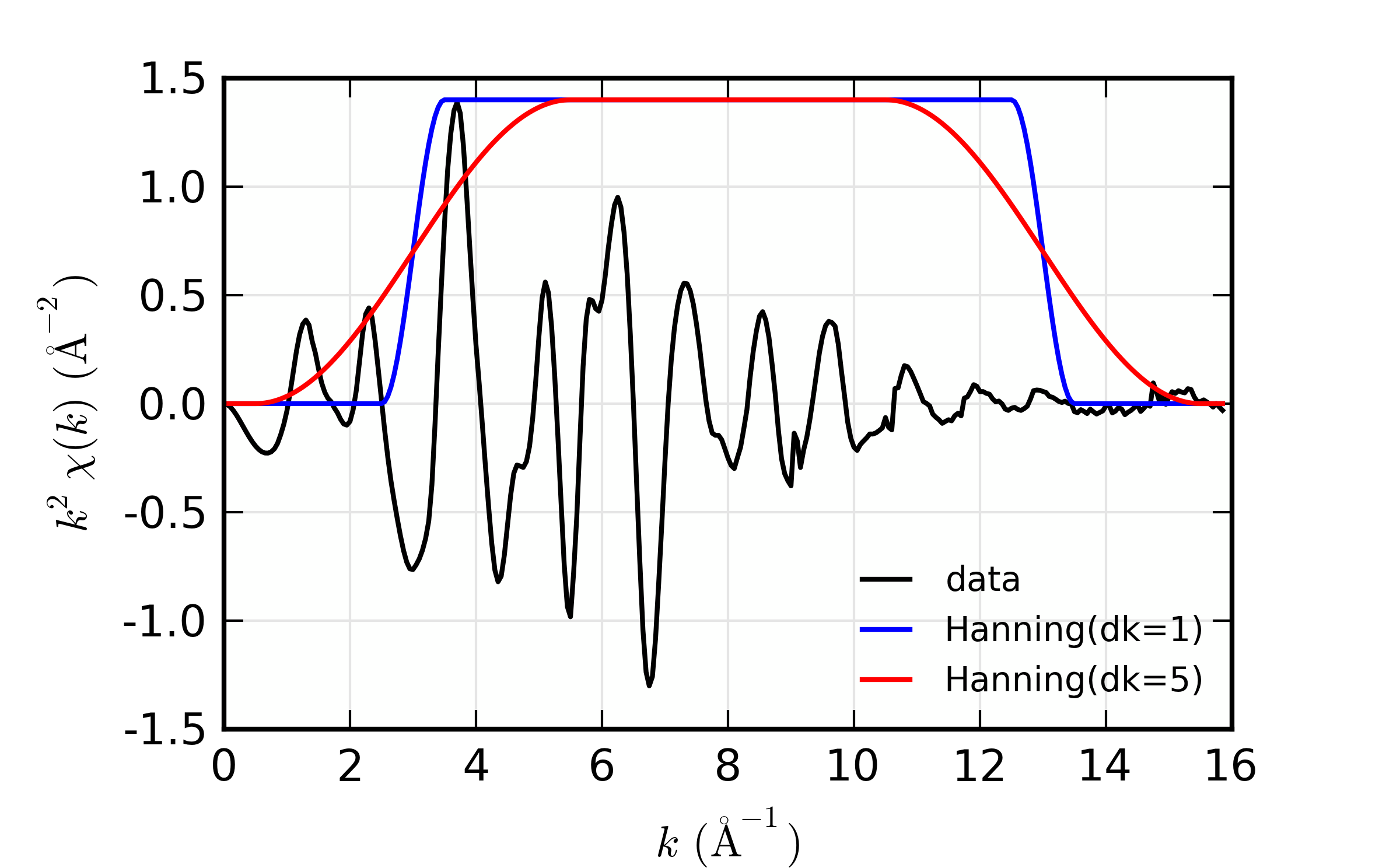

Comparison of the effect of different values of dk on real XAFS
Fourier transforms. Increasing dk reduces peak heights and tends
to broaden peaks, but the effects are rather small.
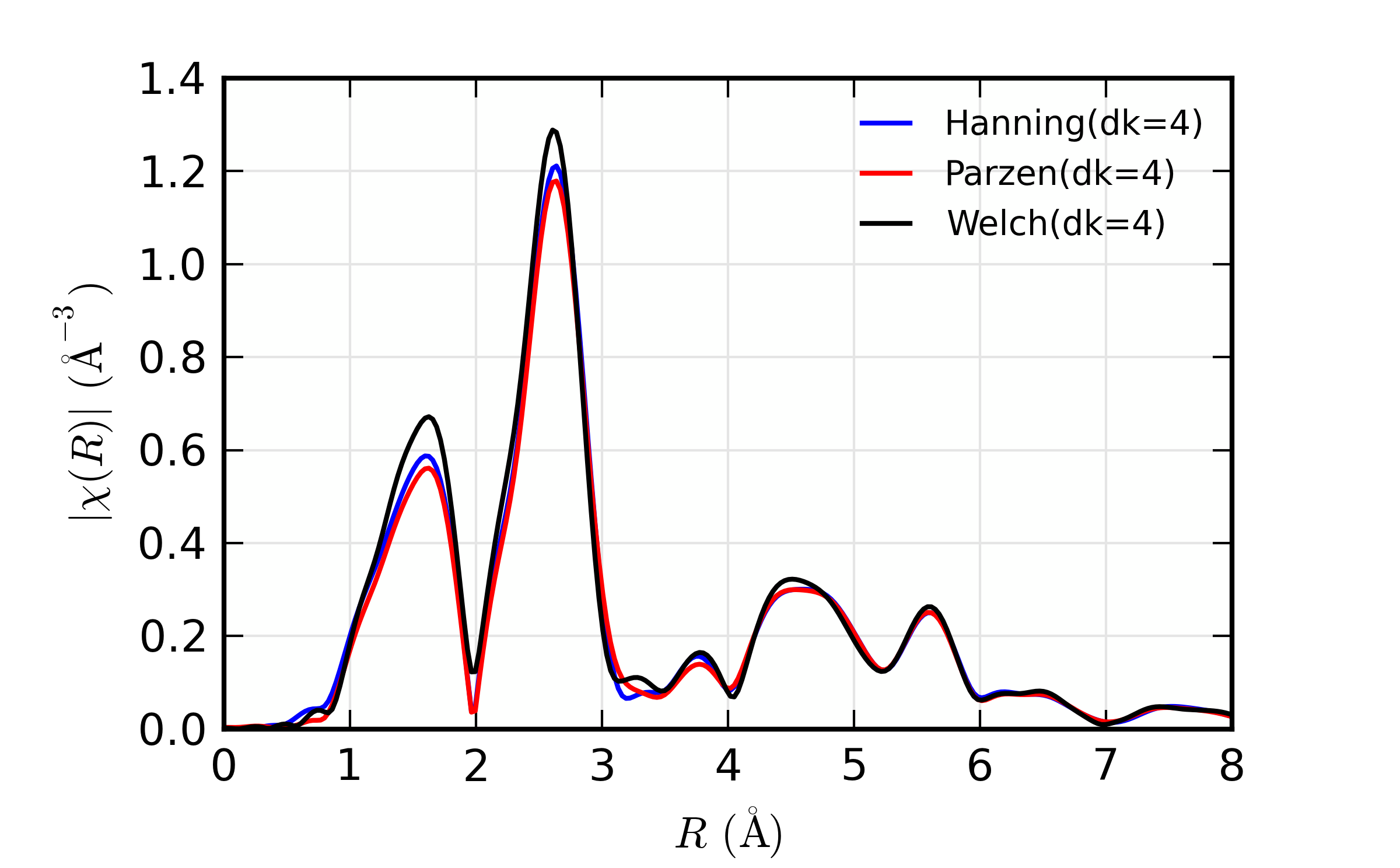
A script that runs xftf() with consistent parameters, but different
window types:
xftf(dat1.k, dat1.chi, kmin=3, kmax=13, dk=4, window='hanning',
kweight=kweight, group=dat1)
dat2 = group(k=dat1.k, chi=dat1.chi) # make a copy of the group
xftf(dat2.k, dat2.chi, kmin=3, kmax=13, dk=4, window='parzen',
kweight=kweight, group=dat2)
dat3 = group(k=dat1.k, chi=dat1.chi) #
xftf(dat3.k, dat3.chi, kmin=3, kmax=13, dk=4, window='welch',
kweight=kweight, group=dat3)
dat4 = group(k=dat1.k, chi=dat1.chi) #
xftf(dat4.k, dat4.chi, kmin=3, kmax=13, dk=4, window='kaiser',
kweight=kweight, group=dat4)
dat5 = group(k=dat1.k, chi=dat1.chi) #
xftf(dat5.k, dat5.chi, kmin=3, kmax=13, dk=4, window='gaussian',
kweight=kweight, group=dat5)
would result in the following results:
We now turn our attention to the different components of the Fourier transform. As above, it is most common to plot the magnitude of the Fourier transform. But, as the transformed \(\chi(R)\) is complex, it can be instructive to plot the real and imaginary components, as shown below:
newplot(dat1.r, dat1.chir_mag, xmax=8, label='chir_mag',
show_legend=True, legend_loc='ur', color='black',
xlabel=r'$R \rm\, (\AA)$', ylabel=r'$\chi(R)\rm\,(\AA^{-3})$' )
plot(dat1.r, dat1.chir_re, color='red', label='chir_re')
plot(dat1.r, dat1.chir_im, color='blue', label='chir_im')
which results in
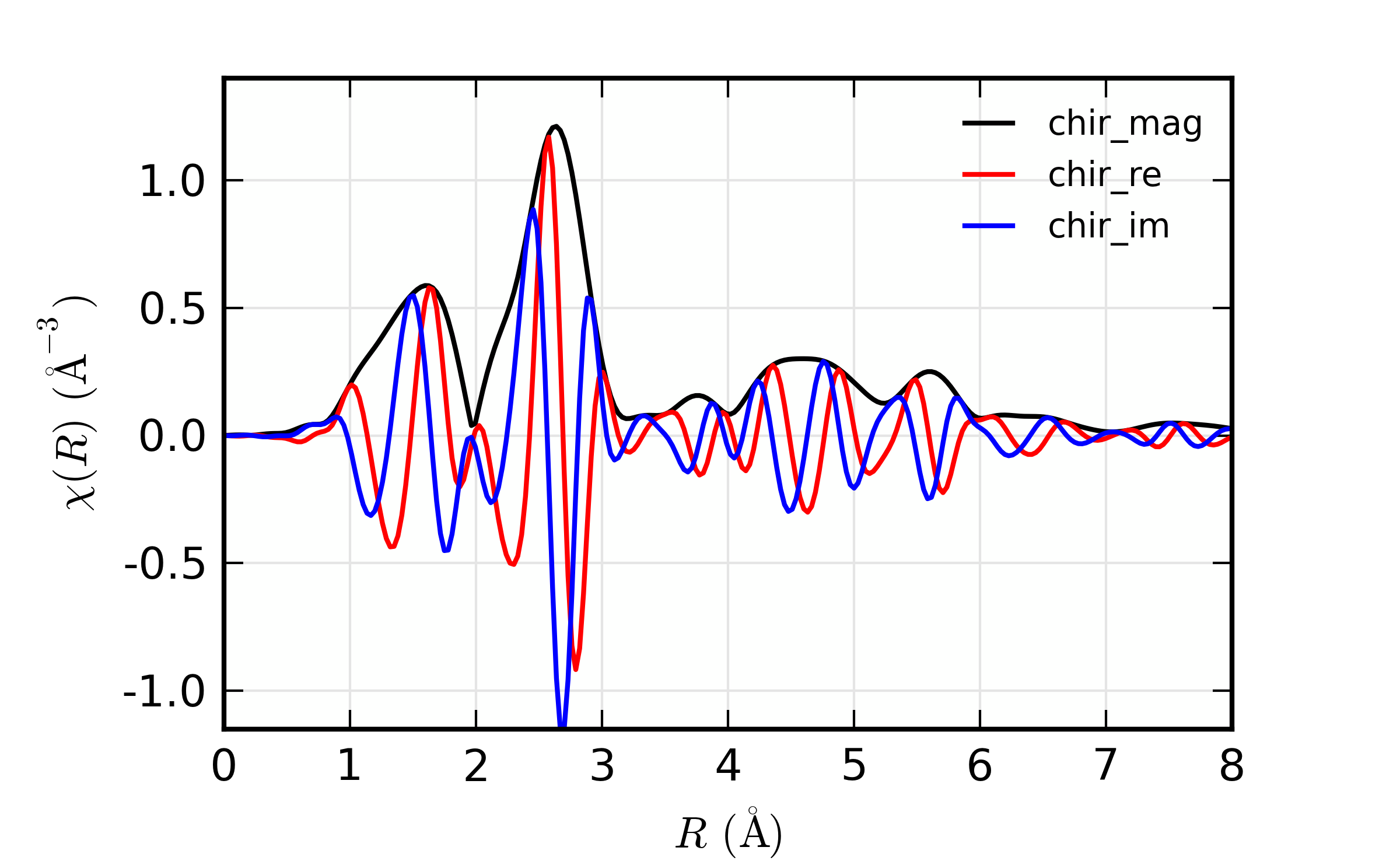
Figure 14.5.6.1 The real and imaginary components of the XAFS Fourier transform.¶
In fact, in the analysis discussed with feffit(), the real and
imaginary components are used, not simply the magnitude.
14.5.7. Examples: Reverse XAFS Fourier transforms, Fourier Filtering¶
A reverse Fourier transform will convert data from \(\chi(R)\) to \(\chi(q)\). This allows a limited range of frequencies (distances) to be isolated and turned back into a \(\chi(k)\) spectrum. Here, we show two different \(R\) windows to filter either just the first shell of the spectra, or the first two shells, and compare the resulting filtered \(\chi(q)\).
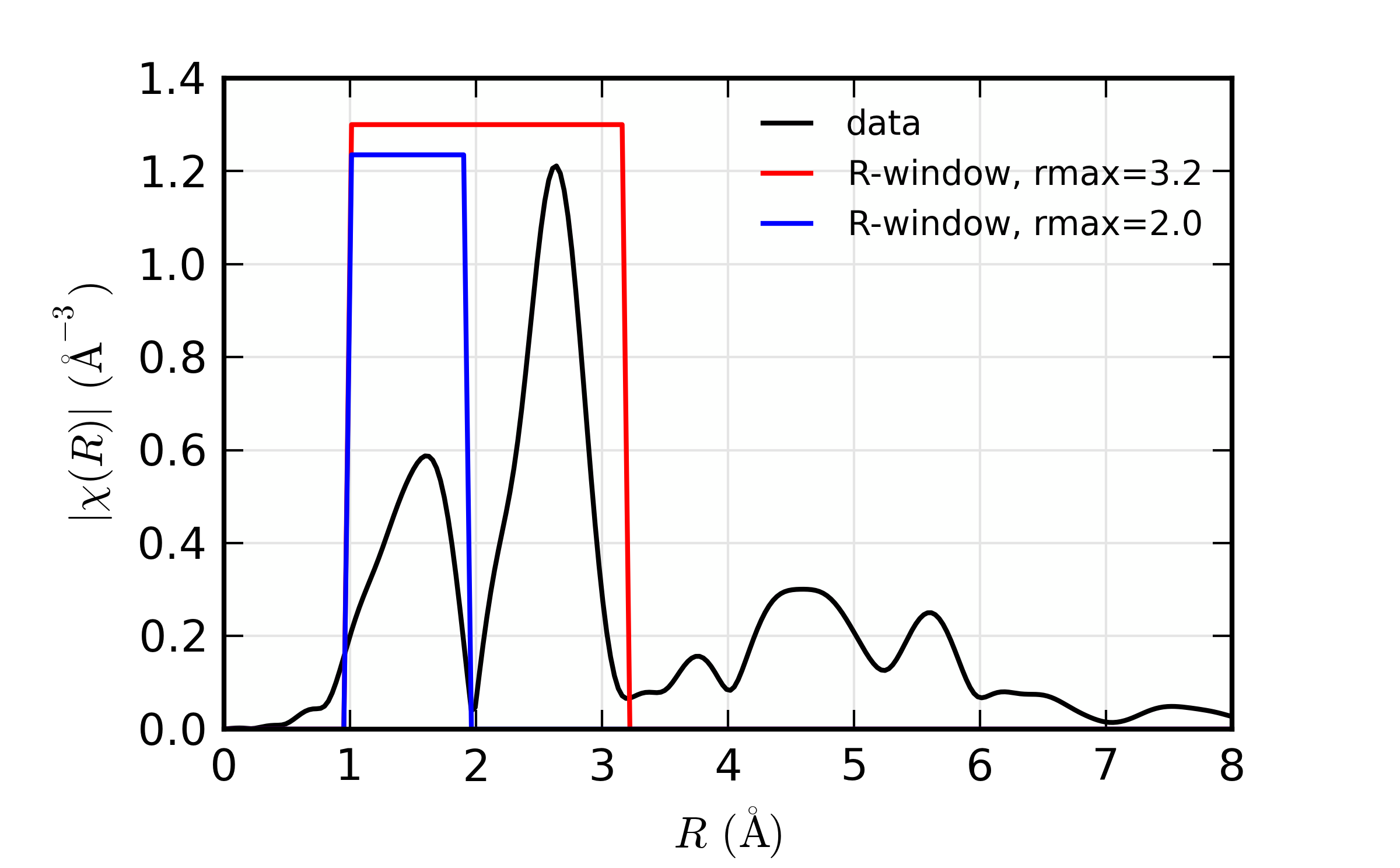
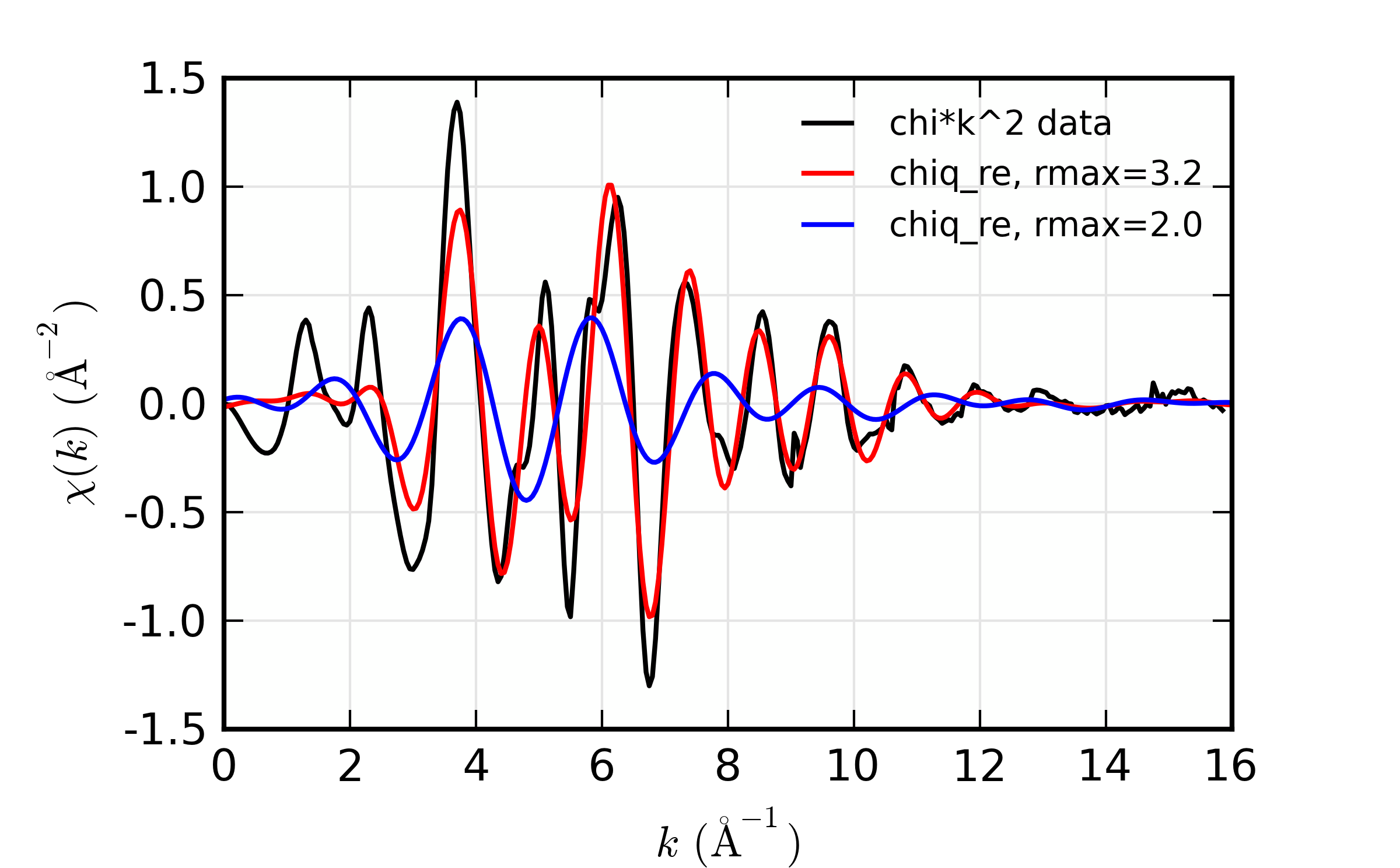
Reverse XAFS Fourier transform, or Fourier filtering. Here, one can see the effect of different window sizes on the Fourier filtered spectrum. Including the first two peaks or shells reproduces most of the original spectrum, with only high-frequency components removed.
Note that it is chiq_re that is compared to the k-weighted chi
array.