\(\newcommand{\AA}{\unicode{x212B}}\)
14.6. XAFS: Wavelet Transforms for XAFS¶
Wavelet transforms extend Fourier transforms, effectively separating
contributions of a waveform into both time and frequency (or, for EXAFS,
\(k\) and \(R\)). A variety of mathematical kernels can be used
for wavelet transforms. There are a few examples in the literature of
applying wavelet transforms to EXAFS data, with the Cauchy wavelet used by
Munoz et al [Munoz, Argoul, and Farges (2003)] being one early application. The
cauchy_wavelet() function described below follows this work, and
that article should be cited as the reference for this transform.
14.6.1. cauchy_wavelet()¶
The Continuous Cauchy Wavelet transform of Munoz et al [Munoz, Argoul, and Farges (2003)]
is implemented as the function cauchy_wavelet():
- cauchy_wavelet(k, chi, group=None, kweight=0, rmax_out=10)¶
perform a Continuous Cauchy wavelet transform of \(\chi(k)\).
- Parameters:
k – 1-d array of photo-electron wavenumber in \(\rm\AA^{-1}\)
chi – 1-d array of \(\chi\)
group – output Group
rmax_out – highest R for output data (10 \(\rm\AA\))
kweight – exponent for weighting spectra by \(k^{\rm kweight}\)
nfft – value to use for \(N_{\rm fft}\) (2048).
- Returns:
None– outputs are written to supplied group.
If a
groupargument is provided of if the first argument is a Group, the following data arrays are put into it:array name
meaning
r
uniform array of \(R\), out to
rmax_out.wcauchy
complex array cauchy transform of \(R\) and \(k\)
wcaychy_mag
magnitude of cauchy transform
wcauchy_re
real part of cauchy transform
wcauchy_im
imaginary part of cauchy transform
It is expected that the input
kbe a uniformly spaced array of values with spacingkstep, starting a 0.
14.6.2. Wavelet Example¶
Applying the Cauchy wavelet transform to Fe K-edge data of FeO is fairly straightforward:
# wavelet transform in larch
# follows method of Munuz, Argoul, and Farges
f = read_ascii('../xafsdata/feo_xafs.dat')
autobk(f, rbkg=0.9, kweight=2)
kopts = {'xlabel': r'$k \,(\AA^{-1})$',
'ylabel': r'$k^2\chi(k) \, (\AA^{-2})$',
'linewidth': 3, 'title': 'FeO', 'show_legend':True}
xftf(f, kmin=1, kmax=14, kweight=2, dk=4.5, window='Kaiser')
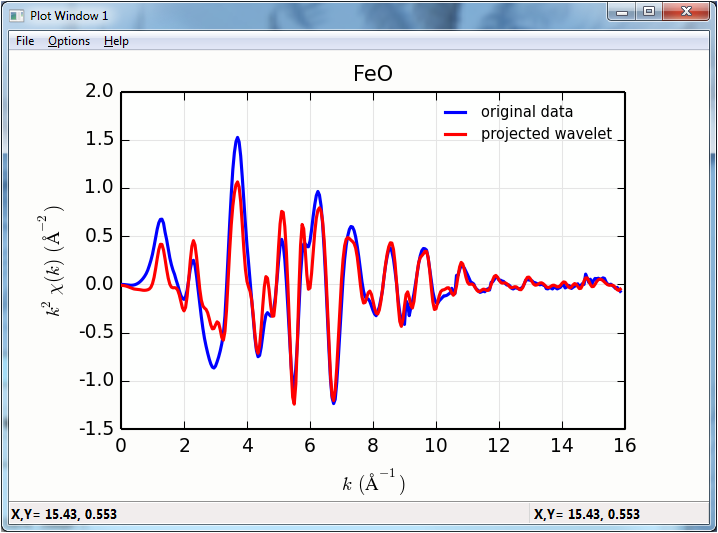
newplot(f.k, f.chi*f.k**2, win=1, label='original data', **kopts)
# do wavelet transform (no window function yet)
cauchy_wavelet(f, kweight=2)
# display wavelet magnitude, real part
# horizontal axis is k, vertical is R
imopts = {'x': f.k, 'y': f.wcauchy_r}
imshow(f.wcauchy_mag, win=1, label='Wavelet Transform: Magnitude', **imopts)
imshow(f.wcauchy_re, win=2, label='Wavelet Transform: Real Part', **imopts)
# plot wavelet projected to k space
plot(f.k, f.wcauchy_re.sum(axis=0), win=1, label='projected wavelet', **kopts)
ropts = kopts
ropts['xlabel'] = r'$R \, (\AA) $'
ropts['ylabel'] = r'$|\chi(R)| \, (\AA^{-3})$'
# plot wavelet projected to R space
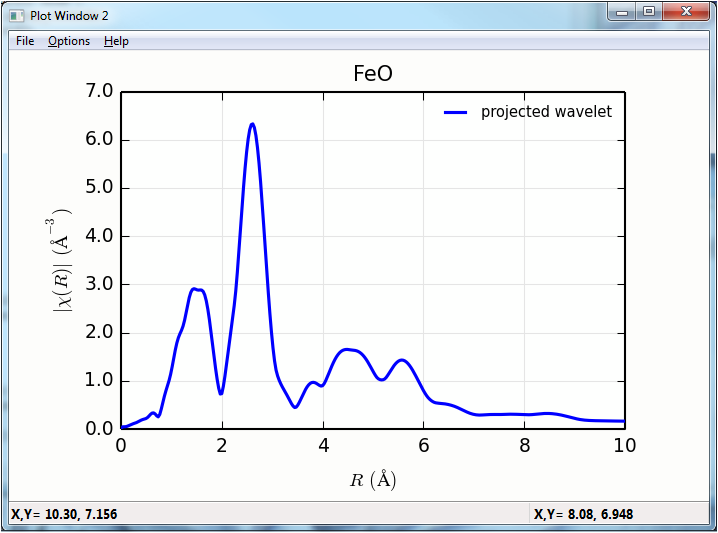
newplot(f.r, f.chir_mag, win=2,
label='traditional XAFS FT', **ropts)
plot(f.wcauchy_r, f.wcauchy_mag.sum(axis=1)/6.0, win=2, label='projected wavelet/6 (?)', **ropts)
With results for the Cauchy transforms looking like (here, \(k\)is along the horizontal axis extending to 16 \(\rm\AA^{-1}\), and with \(R\) along the vertical axis, increasing from 0 at the bottom to 10 \(\rm\AA\) at the top.


The Cauchy Wavelet transforms, with magnitude on the left hand panel and real part on the right hand panel.
The projection of the wavelets to \(k\) and \(R\) space looks like: