\(\newcommand{\AA}{\unicode{x212B}}\)

14.7. XAFS: Reading and using Feff Paths

For modeling EXAFS data, Larch relies heavily on calculations of theoretical XAFS spectra using Feff. Being able to run Feff and use its results is of fundamental importance for using Larch for fitting EXAFS spectra. While a complete description of Feff ([Rehr et al. (1991)], [Zabinsky et al. (1995)], [Rehr and Albers (2000)]) is beyond the scope of this documentation, here we describe how to read the results from Feff into Larch.

The funcionality of Feff within Larch has been evolving to better incorporate Feff8l into Larch. Feff8L provideds a free version of Feff Version 8.5 for EXAFS calculations (not XANES or other spectroscopies), and is being developed in parallel to Larch at feff85exafs [1]. Part of the goal for this project is to replace Feff Version 6l as a robust and easy-to-use EXAFS calculation engine for EXAFS Analysis. A larger goal for feff85exafs and Larch is to be able to create the potentials and scattering factors needed for the EXAFS calculation, and then to be able to use that to dynamically create EXAFS scatternig paths with changing geometries. This is a work-in-progress. If you’re interested in exploring or helping with this, contact us!

The main interface for this is the feffpath() function that reads feffNNNN.dat file and creates a FeffPath Group.

14.7.1. Running Feff

Larch comes with external programs for Feff6l and Feff8l, and provides two simple functions for running the external Feff6l andFeff8l programs from within Larch: feff6l() and feff8l(). Note that the input files for these two programs are similar but have important differences in syntax such that the input for one cannot be used for running the other.

14.7.1.1. Running Feff6l with feff6l()

feff6l(folder='.', feffinp='feff.inp', verbose=True)

run Feff6 in the supplied folder.

Parameters:

• folder – name of folder containing the Feff6 input file, and where to put the output files [‘.’, the current working directory]

• feffinp – name of feff.inp file within the supplied folder [‘feff.inp’]

• verbose – flag controlling screen output from Feff [True]

Returns:

a FeffRunner Group.

This will generate a number of outputs, including the feffNNNN.dat files containing the data for each scattering path.

14.7.1.2. Running Feff8l with feff8l()

feff8l(folder='.', feffinp='feff.inp', verbose=True)

run Feff8L in the supplied folder.

Parameters:

• folder – name of folder containing the Feff6 input file, and where to put the output files [‘.’, the current working directory]

• feffinp – name of feff.inp file within the supplied folder [‘feff.inp’]

• verbose – flag controlling screen output from Feff [True]

Returns:

a FeffRunner Group.

As with feff6l(), this will generate a number of outputs, including the feffNNNN.dat files containing the data for each scattering path.

14.7.1.3. Running Feff8l with feffrunner()

The incorporation of Feff8l in Larch is still in development, but is ntended to make the executables from the feff85exafs package easy to use and a seamless drop-in replacement for Feff6l. The FeffRunner tool is quite flexible and can be used to run specific modules from feff85exafs or other versions of Feff that you might have on your computer.

feffrunner(feffinp=None, verbose=True, repo=None)

create a FeffRunner Group from a feff.inp file.

Parameters:

• feffinp – name (full path of) feff.inp file

• verbose – flag controlling screen output from Feff [True]

• repo – full path of the location of the Feff8l repository [None]

Returns:

a FeffRunner Group.

feffrunner.run(exe)

run Feff for FeffRunner Group.

Parameters:

exe – the name of the Feff program to be run [run all of Feff8l]

Returns:

None when Feff is run successfully or an Exception when a problem in encoiuntered

The simplest example of its use is

feff = feffrunner('path/to/feff.inp')
feff.run()

The feff.inp file is specified when the Group is created, then feff85exafs is run in the same folder as the feff.inp file. In this case, since no argument is given to the run() method, the various modules of feff85exafs are run in sequence. This behaves much like the monolithic Feff executables of yore.

The feff85exafs modules (rdinp, pot, xsph, pathfinder, genfmt, and ff2x) can be be run individually

feff = feffrunner('path/to/feff.inp')
feff.run('rdinp')
feff.run('pot')
## and so on ...

To specifically use the feff85exafs modules from a local copy of the feff8l repository, do

feff = feffrunner('path/to/feff.inp')
feff.repo = '/home/bruce/git/feff85exafs'
feff.run()

The repo attribute is used when working on feff85exafs itself. For example, the feff85exafs unit tests set the repo attribute so that the just-compiled versions of the programs get used.

If you have an executable for some other version of Feff in a location that in your shell’s execution path and it is called something like feff6, feff7, or any other name than begins with feff, that can be run as

feff = feffrunner('path/to/feff.inp')
feff.run('feff6') # or whatever your executable is called

If the _xafs._feff_executable symbol in Larch’s symbol table is set to a valid executable, then you can use that by doing

feff = feffrunner('path/to/feff.inp')
feff.run(None)

The feff.inp file need not be called by that name. FeffRunner will copy the specified file to feff.inp in the specified folder – taking care not to clobber an existing feff.inp file – before running Feff. Once finished, it will copy files back to their original names.

A log file called f85e.log is written in the same folder as the feff.inp. This log file captures all of the screen output (both STDOUT and STDERR) from Feff.

The full structure of the FeffRunner group looks something like this:

== External Feff Group: Copper/testrun/feff.inp: 5 symbols ==
  feffinp: 'Copper/testrun/feff.inp'
  repo: None
  resolved: '/usr/local/bin/ff2x'
  run: <bound method FeffRunner.run of <External Feff Group: Copper/testrun/feff.inp>>
  verbose: True

The resolved attribute has the fully resolved path to the most recently run executable. This can be used to verify that the logic for executable resolution described above worked as intended.

14.7.2. feffpath() and FeffPath Groups

The outputs from Feff for each path are complicated enough to need a structured organization of data. This is accomplished by providing a special kind of a Larch Group – a FeffPath Group which holds all the information about a Feff Path, including the photo-electron scattering amplitudes and phase-shifts needed to describe and calculate the EXAFS for that Path. A FeffPath Group is created with the feffpath() group. For many uses a Feff Path can be treated as a “black box”, and simply setting the adjustable Path Parameters and passing around these Groups is sufficient for simulating and fitting EXAFS spectra.

At times it can be helpful to inspect and study the detailed components of the Feff Path. Since a FeffPath Group is a regular Larch Group, all the data can be read and viewed. A FeffPath Group has the components listed in the Table of Feff Path Parameters. This includes the Adjustable Numerical Path Parameters – the values of which can be changed to affect the calculated EXAFS for the Path – as well as the arrays for \(k\) and \(\chi\) and several other attributes. Since this Group is used to calculate \(\chi(k)\) for the path, many of the components need to be in place and holding the expected values so that the calculation can be done correctly, Due to Larch’s flexibility, it is possible to delete, overwrite, or put inappropriate values into the components of a FeffPath Group, and care must be taken to avoid this.

Table of FeffPath Parameters, including the Path Parameters used in the EXAFS equation. The attributes here are arranged by category. The Info attributes are informational only. The two Numerical attributes reff and nleg are used in the EXAFS equation but are meant to be constants and their values should not be changed. The Adjustable attributes are the standard Adjustable, Numerical Path Parameters that can be changed to affect the resulting EXAFS \(\chi(k)\). These can be set either as constant values or fitting Parameters as defined by _math.param(). The Output array attributes are the arrays output from path2chi(). Finally, the sub-group _feffdat contains the low-level data as read directly from the feffNNNN.dat file, which is detailed in the next section, The _feffdat Group: Full Details of the Feff.Dat File.

attribute name	category	description
filename	Info	name of feffNNNN.dat file
label	Info	path description
geom	Info	path geometry: list of (symbol, ipot, x, y, z)
reff	Numerical	\(R_{\rm eff}\), nominal path length
nleg	Numerical	number of path legs (1+number of scatterers)
degen	Adjustable	\(N\), path degeneracy
s02	Adjustable	\(S_0^2\), amplitude reduction factor
e0	Adjustable	\(E_0\), energy origin
deltar	Adjustable	\(\Delta R\), shift in path length
sigma2	Adjustable	\(\sigma^2\), mean-square displacement
third	Adjustable	\(c_3\), third cumulant
fourth	Adjustable	\(c_4\), the fourth cumulant
ei	Adjustable	\(E_i\), imaginary energy shift.
k	Output array	\(k\), photo-electron wavenumber
chi	Output array	\(\chi\), the EXAFS
chi_imag	Output array	\(\rm{Im}(\chi)\), imaginary EXAFS
p	Output array	\(p\), complex photo-electron wavenumber
_feffdat	Group	a Group containing raw data from feffNNNN.dat

feffpath(filename, label=None, s02=None, degen=None, e0=None, deltar=None, sigma2=None, ...)

create a FeffPath Group from a feffNNNN.dat file.

Parameters:

• filename – name (full path of) feffNNNN.dat file

• label – label for path [file name]

• degen – path degeneracy, \(N\) [taken from file]

• s02 – \(S_0^2\) value or parameter [1.0]

• e0 – \(E_0\) value or parameter [0.0]

• deltar – \(\Delta R\) value or parameter [0.0]

• sigma2 – \(\sigma^2\) value or parameter [0.0]

• third – \(c_3\) value or parameter [0.0]

• fourth – \(c_4\) value or parameter [0.0]

• ei – \(E_i\) value or parameter [0.0]

Returns:

a FeffPath Group.

For all the options described above with value or parameter either a numerical value or a Parameter (as created by _math.param()) can be given.

14.7.3. path2chi() and ff2chi(): Generating \(\chi(k)\) for a FeffPath

path2chi(path, paramgroup=None, kmax=None, kstep=0.05, k=None)

calculate \(\chi(k)\) for a single Feff Path.

Parameters:

• path – a FeffPath Group

• paramgroup – a Parameter Group for calculating Path Parameters [None]

• kmax – maximum \(k\) value for \(\chi\) calculation [20].

• kstep – step in \(k\) value for \(\chi\) calculation [0.05].

• k – explicit array of \(k\) values to calculate \(\chi\).

Returns:

None

If k is specified, that will be used as the set of \(k\) values at which to calculate \(\chi\). If not given, the values of kstep and kmax will be used to construct a uniformly-spaced array of \(k\) values starting at 0 and extending to (and including) kmax.

The calculated \(\chi\) array is placed in the Feff Path Group path as path.chi. In addition calculated arrays for \(k\), \(p\), and \(\rm{Im}(\chi)\) are placed in the variables path.k, path.p, and path.chi_imag, respectively. See The EXAFS Equation using Feff and FeffPath Groups for the detailed definitions of the quantities.

If specified, paramgroup is used as the Parameter Group – the group used for evaluating parameter expressions (ie, constraints using named variables). This is similar to the use for _math.minimize() as discussed in Parameters.

ff2chi(pathlist, paramgroup=None, group=None, k=None, kmax=None, kstep=0.05)

sum the \(\chi(k)\) for a list of FeffPath Groups.

Parameters:

• pathlist – a list of FeffPath Groups

• paramgroup – a Parameter Group for calculating Path Parameters [None]

• group – a Group to which the outputs are written [None]

• kmax – maximum \(k\) value for \(\chi\) calculation [20].

• kstep – step in \(k\) value for \(\chi\) calculation [0.05].

• k – explicit array of \(k\) values to calculate \(\chi\).

Returns:

None

This essentially calls path2chi() for each of the paths in the pathlist and writes the resulting arrays for \(k\) and \(\chi\) the sum of \(\chi\) for all the paths) to group.k and group.chi.

14.7.4. The _feffdat Group: Full Details of the Feff.Dat File

Each FeffPath Group will have a _feffdat sub-group which contains the data from the underlying feffNNNN.dat file for the results of the Feff calculation. Many of the components of this group are used for the calculations of \(\chi(k)\) for that Path, though some (such as exch and edge) are kept only for informational purposes. Some components from this sub-group (notably as geom and nleg) are copied into the FeffPath Group. As with the FeffPath Group, this Group has an expected set of components that should be treated as read-only unless you really know what you’re doing.

Table of Feff.dat components. Listed here is the component read from the Feff.dat file and stored in the _feffdat group for each FeffPath.

attribute	description
amp	array: total amplitude, \(F_{\rm eff}(k)\)
degen	path degeneracy (coordination number)
edge	energy threshold relative to atomic valu (a poor estimate)
exch	string describing electronic exchange model
filename	File name
gam_ch	core level energy width
geom	path geometry: list of (Symbol, Z, ipot, x, y, z)
k	array: k values, \(k_{\rm feff}\)
kf	k value at Fermi level
lam	array: mean-free path, \(\lambda(k)\)
mag_feff	array: magnitude of Feff
mu	Fermi level, eV
pha	array: total phase shift, \(\delta(k)\)
pha_feff	array: scattring phase shift
potentials	path potentials: list of (ipot, z, r_MuffinTin, r_Norman)
real_phc	array: central atom phase shift
red_fact	array: amplitude reduction factor
rep	array: real part of p, \(p_{\rm real}(k)\)
rnorman	Norman radius
rs_int	interstitial radius
title	user title
version	Feff version
vint	interstitial potential

The arrays from the data columns of the Feff data file break up the amplitude and phase into two components (essentially as one for the central atom and one for the scattering atoms) that are simply added together. Thus amp = red_fact + mag_feff and the sum is used as \(F_{\rm eff}(k)\). Similarly, pha = real_phc + pha_feff and the sum is used as \(\delta(k)\).

14.7.5. The EXAFS Equation using Feff and FeffPath Groups

Now we are ready to write down the full EXAFS equation used for a Feff Path using the terms defined above in the Table of Feff Path Parameters and the Table of Feff.Dat Components. One of the trickier concepts is that we are evaluating at experimental values of \(k\) while the Feff calculation is tabulated on its own set of \(k\) values and we may need to apply an energy shift of \(E_0\) to the Feff calculation. Thus, first we find \(k\) as

\[k = \sqrt{k_{\rm feff}^2 - {2m_e E_0}/{\hbar^2} }\]

where \(E_0\) is taken from the e0 parameter and \(k_{\rm feff}\) are the \(k\) values from Feff (_feffdat.k). This shifted \(k\) will be used to access the \(k\) dependent values from the Feff arrays. Next, we note that we need the complex wavenumber, defined as

\[p = p' + i p'' = \sqrt{ \big[ p_{\rm real}(k) - i / \lambda(k) \big]^2 - i \, 2 m_e E_i /{\hbar^2} }\]

where \(p_{\rm real}\) and \(\lambda\) are the values from Feff (_feffdat.rep and _feffdat.lam) and \(E_i\) is the complex energy shift from the parameter ei. Note that \(i\) is used as the complex number following the physics literature, while within Larch 1j is used. The complex wavenumber \(p\) includes a self-energy term (due to the presence of multiple electrons in the system) and is meant to be referenced to the absorption threshod while \(k\) is meant to be referenced to the Fermi level. Thus \(p_{\rm real} \approx \Sigma + k\), where \(\Sigma\) is a small but usually positive offset. Within the EXAFS equation, \(k\) is used to restore the calculation of \(\chi(k)\) as done by Feff, while \(p\) is used to apply alterations to \(\chi(k)\) as for disorder terms.

The EXAFS equation used for constructing \(\chi(k)\) from a Feff calculation is then

\begin{eqnarray*} \chi(k) = & {\rm Im}\Bigl[ {\displaystyle{ \frac{f_{\rm eff}(k) N S_0^2} {k(R_{\rm eff} + \Delta R)^2} } \exp(-2p''R_{\rm reff} - 2p^2\sigma^2 + \textstyle{\frac{2}{3}}p^4 c_4)} \hspace{18mm} \,\, \\ &{\times \exp \bigl\{ i\big[ 2kR_{\rm eff} + \delta(k) + 2p(\Delta R - 2\sigma^2/R_{\rm eff} ) - \textstyle{\frac{4}{3}} p^3 c_3 \big] \bigr\} } \Bigr] \\ \end{eqnarray*}

where the terms are all defined above. Again, note that \(k\) is used to reconstruct the unaltered EXAFS from the Feff.dat file, and the complex \(p\) is used for the terms adding the effects of disorder. Also note that \(p''\) becomes \(\lambda(k)\) for \(E_i = 0\), and is the generalization of the mean-free-path contribution. The terms \(\Delta R\), \(\sigma^2\), \(c_3\), and \(c_4\) are the first four cumulants of the atomic pair distribution for the selected path. The additional term \(-2p(2\sigma^2/R_{\rm eff})\) in the phase is a correction to the cumulant expansion due to the averaging over the \(1/R^2\) term in the EXAFS equation.

The use of the cumulant expansion here does not necessarily imply that systems must be ordered enough for their atomic distributios to modeled by the cumulant expansion. All that is required is that contribution from each path be ordered enough for the cumulant expansion to work. A highly disordered system can be modeled by applying a more complex weighting to a set of paths – that is, a histogram of paths.

14.7.6. Models for Calculating \(\sigma^2\)

The value for \(\sigma^2\) in the EXAFS equation gets a lot of attention in the EXAFS literature, as it is often the only term used to account for thermal and static disorder in an ensemble of Paths that makes up a full EXAFS spectra. Borrowing from Feff (see [Rehr et al. (1991)], [Sevillano, Meuth, and Rehr (1979)] and [Rehr and Albers (2000)]) Larch provides two functions that use simple models to calculate \(\sigma^2\) for a Path. Both functions, sigma2_eins() and sigma2_debye() take arguments of sample temperature, a characteristic temperature, and a FeffPath, and return a value of \(\sigma^2\). These are known to appy reasonably well to very simple systems (such as metals and solids with few atomic components), and less well to complex systems, including anything with organic ligands.

..versionchanged:: 0.9.34

removed _sys.paramGroup, now using fiteval

sigma2_eins(t, theta)

calculate \(\sigma^2\) in the Einstein model.

Parameters:

• t – sample temperature (in K)

• theta – Einstein temperature (in K)

• path – a FeffPath Group [None]

The path argument can be left None. This will try to use the ‘’current FeffData group”, (_sys.fiteval.symtable._feffdat), which is updated during fits with feffit() and when summing paths with ff2chi().

sigma2_debye(t, theta, path=None)

calculate \(\sigma^2\) in the Debye model.

Parameters:

• t – sample temperature (in K)

• theta – Debye temperature (in K)

• path – a FeffPath Group [None]

As with sigma2_eins, the `path() argument can be left None, and the ‘’current FeffData group”, (_sys.fiteval.symtable._feffdat), will be used.

14.7.7. Example: Reading a Feff file

Here we simply read a feffNNNN.dat file and display its components, and calculate \(\chi\) for this path with two different values of \(\sigma^2\).

## examples/feffit/doc_feffdat1.lar

fname = 'feff0001.dat'
path1 = feffpath(fname)

path2chi(path1)
show(path1)


newplot(path1.k, path1.chi*path1.k**2, xlabel=r' $ k \rm\, (\AA^{-1})$',
        ylabel=r'$ k^2\chi(k)$', label = r'$\sigma^2 = 0$', show_legend=True,
        title=r'$\chi(k)$ from %s' % fname)

path1.sigma2 = 0.002

path2chi(path1)

plot(path1.k, path1.chi*path1.k**2, label = r'$\sigma^2 = 0.002$')

## end examples/feffit/doc_feffdat1.lar

The output of this looks like this:

== FeffPath Group feff0001.dat: 16 symbols ==
  _feffdat: <Feff.dat File Group: feff0001.dat>
  chi: array<shape=(401,), type=dtype('float64')>
  chi_imag: array<shape=(401,), type=dtype('float64')>
  degen: 12.0
  deltar: 0
  e0: 0
  ei: 0
  filename: 'feff0001.dat'
  fourth: 0
  geom: [('Cu', 29, 0, 0.0, 0.0, 0.0), ('Cu', 29, 1, 0.0, -1.8016, 1.8016)]
  k: array<shape=(401,), type=dtype('float64')>
  label: 'feff0001.dat'
  p: array<shape=(401,), type=dtype('complex128')>
  s02: 1
  sigma2: 0
  third: 0

After the initial read, the values of k, p, chi, and chi_imag are set to None, and are not calculated until path2chi() is called.

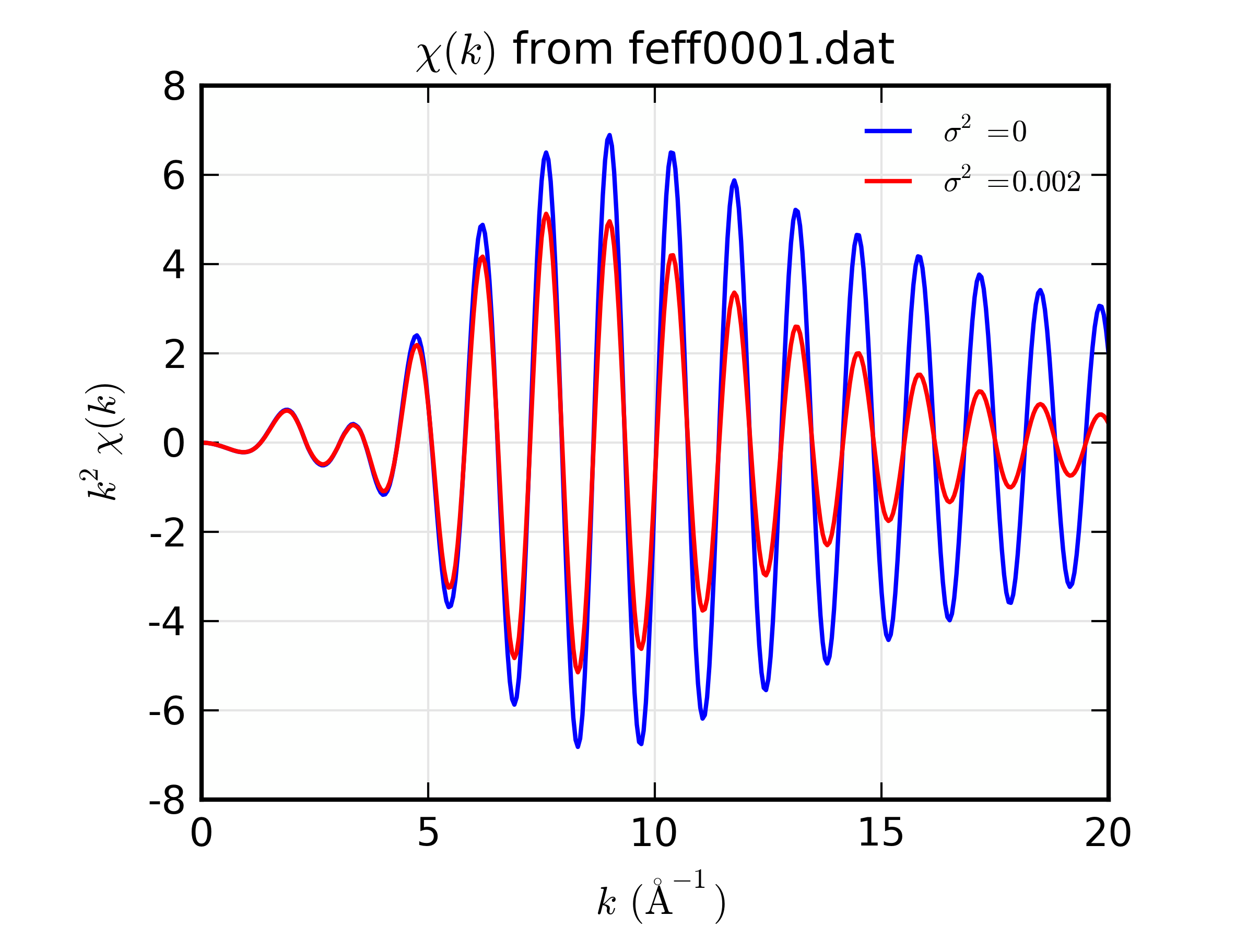
Figure 14.7.7.1 Calculations of \(\chi(k)\) for a Feff Path.

We can also use the data from the _feffdat group to look at the individual scattering components. Thus to look at the scattering amplitude and mean-free-path for a particular scattering path, you could use a script like this:

## examples/feffit/doc_feffdat2.lar

fname = 'feff0001.dat'
path1 = feffpath(fname)

newplot(path1._feffdat.k, path1._feffdat.amp, xlabel=r' $ k \rm\, (\AA^{-1})$',
        ylabel=r'$ |F_{\rm eff}(k)|$', label = r'amp', show_legend=True,
        title=r'components of _feffdat for %s' % fname,
        marker='o', markersize=4)

plot(path1._feffdat.k, path1._feffdat.lam, side='right',
     marker='o', markersize=4,
     label = r'lam', y2label=r'$ \lambda(k) \rm\, (\AA)$')

## end examples/feffit/doc_feffdat2.lar

which will produce a plot like this:

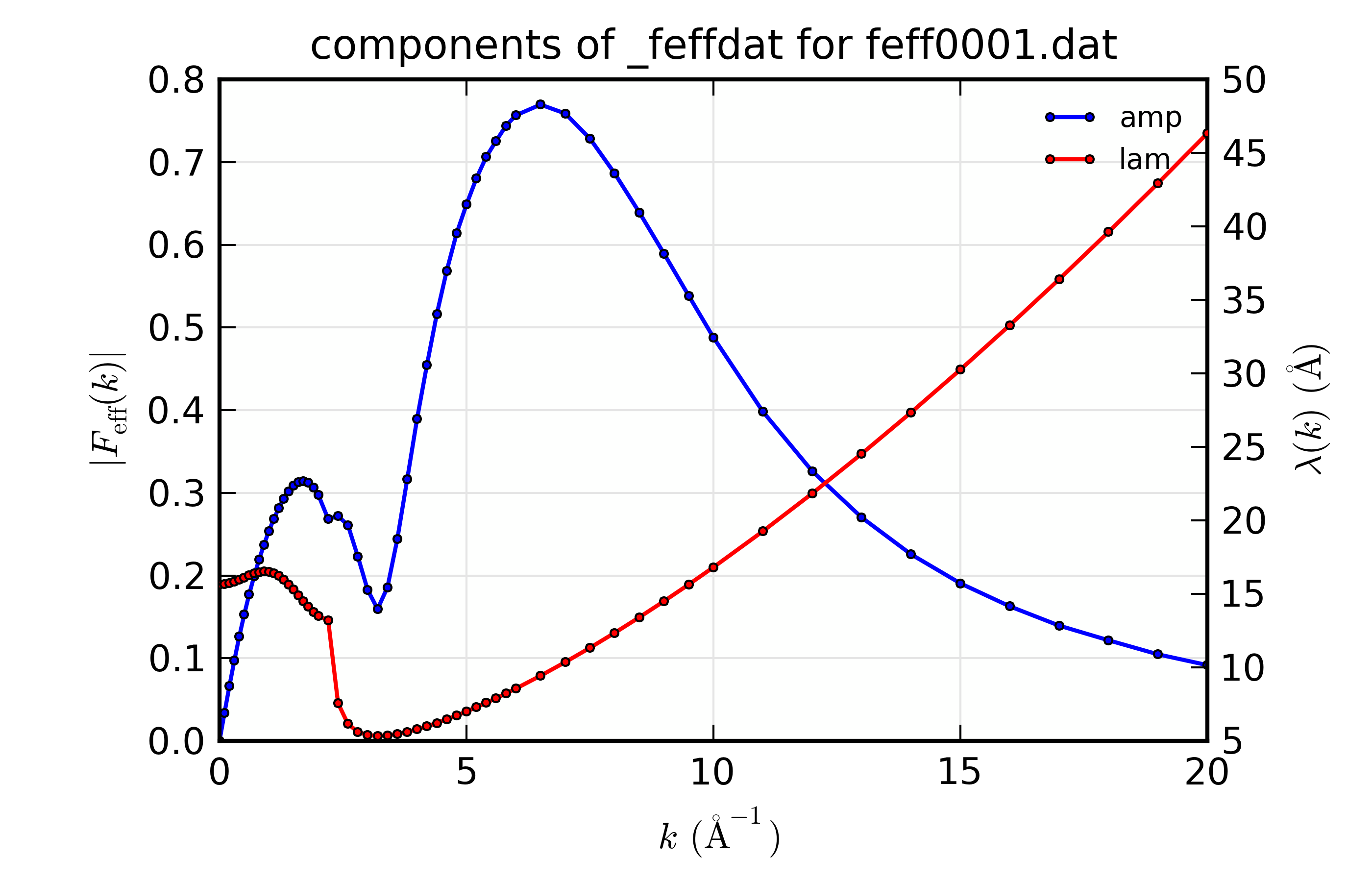
Figure 14.7.7.2 Components of _feffdat group for a Feff Path.

You can see here that the arrays in the _feffdat group are sampled at varying \(k\) spacing, and that this spacing becomes fairly large at high \(k\).

14.7.8. Example: Adding Feff files

Now, we add some Feff files together, applying some path parameters. The example is actually very similar to the one above except that we use ff2chi() to create a \(\chi(k)\) from a list of paths, and put the result into its own group. Thus:

## examples/feffit/doc_feffdat3.lar

# read some paths
path1 = feffpath('feff_feo01.dat')
path2 = feffpath('feff_feo02.dat')
path3 = feffpath('feff_feo03.dat')
path4 = feffpath('feff_feo04.dat')
path5 = feffpath('feff_feo05.dat')

# apply an e0 shift and s02 to all paths:
for p in (path1, path2, path3, path4, path5):
    p.e0  = -0.5
    p.s02 =  0.9
endfor

path1.sigma2 = 0.003
path2.sigma2 = 0.004
path3.sigma2 = 0.006
path4.sigma2 = 0.008
path5.sigma2 = 0.008
mysum = group(label='FeO sum of paths 1,2,3,4,5')

ff2chi([path1, path2, path3, path4, path5], group=mysum)

## now, we can also simply sum paths 3,4,5...
mysum.chi345 = path3.chi + path4.chi + path5.chi


newplot(mysum.k, mysum.chi*mysum.k**2, label='sum(1,2,3,4,5)', show_legend=True,
        xlabel=r' $ k \rm\, (\AA^{-1})$',
        ylabel=r'$ k^2\chi(k)$',  title=mysum.label)

plot(path1.k, -2.+path1.chi*path1.k**2, label='path1')
plot(path2.k, -4+path2.chi*path2.k**2, label='path2')
plot(path3.k, -6+mysum.chi345*path3.k**2, label='sum(3,4,5)')

## end examples/feffit/doc_feffdat3.lar

With the result as shown below. Note that we can also make a simple sum of a set of paths, which was done in this example to add the contributions of paths 3, 4, and 5. This works because ff2chi() runs path2chi() for each path to be summed, so that the chi component of the FeffPath group is up to date.

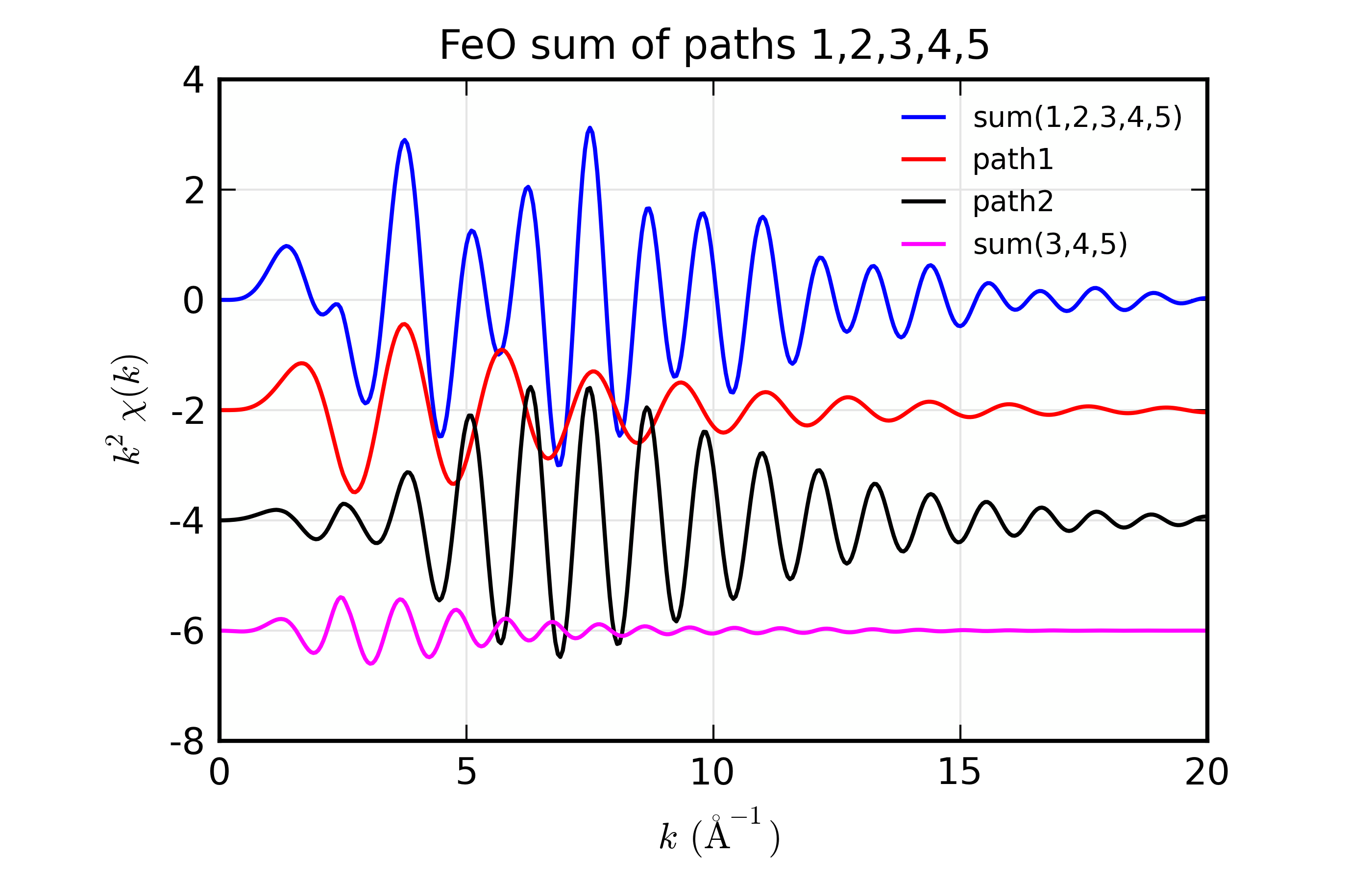
Figure 14.7.8.1 Results for sum of \(\chi(k)\) for list of paths.

14.7.9. Example: Using Path Parameters when adding Feff files

Using Parameters for modelling data is a key feature of Larch, and if you are modelling XAFS data with Feff, you will want to parameterize Path Parameters, apply them to a set of Paths, and investigate the resulting sum of Paths. This is similar to the examples above, but combines the Parameter concept from the Fitting chapter. In Larch, this looks like:

## examples/feffit/doc_feffdat4.lar

# read some paths
path1 = feffpath('feff_feo01.dat')
path2 = feffpath('feff_feo02.dat')

# create a group containing parameters
pars = group(del_e0 = param('del_e0', -4.0, min=-10, max=10),
             amp= param('amp', 0.8, min=0.3, max=1.5))

for p in (path1, path2):
    p.e0  = 'del_e0'
    p.s02 = 'amp'
    p.sigma2 = 0.003
    if p == path2:
        p.sigma2 = 0.005
    #endif
#endfor

mysum = group(label='FeO sum of paths')

ff2chi([path1, path2], group=mysum, paramgroup=pars)

label='E0=%.1f, S02=%.1f' % (pars.del_e0.value, pars.amp.value)

newplot(mysum.k, mysum.chi*mysum.k**2,
        label=label, show_legend=True,
        xlabel=r'$ k \rm\, (\AA^{-1})$',
        ylabel=r'$ k^2\chi(k)$',  title=mysum.label)


# now change parameter values, re-do sum
pars.del_e0.value = 3.5
pars.amp.value = 0.95

# re-calculate chi for each path with paramgroup set
# then sum the paths ourselves
path2chi(path1, paramgroup=pars)
path2chi(path2, paramgroup=pars)

mysum.chi_alt = path1.chi + path2.chi

label='E0=%.1f, S02=%.1f' % (pars.del_e0.value, pars.amp.value)
plot(mysum.k, mysum.chi_alt*mysum.k**2, label=label)

## end examples/feffit/doc_feffdat4.lar

After reading in the Feff data files, we have created a group pars of Parameters with _math.param(), specifically pars.del_e0 and pars.amp. Then we set the e0 path parameter for each path to the string 'del_e0', and the amp path parameter to 'amp'. We set the sigma2 values to simple numbers, as above.

Now, when running ff2chi(), we give not only a group to put the results in, but also a paramgroup to use as the parameters for evaluating any mathematical expressions we’ve defined for the path parameters. At this point, the strings del_e0 and amp for the path parameters for path 1 and 2 are converted into Parameters and evaluated.

..versionchanged:: 0.9.34

removed _sys.paramGroup, now using fiteval

After plotting the results, we then change the values of the parameters. We could re-run ff2chi(), but we can also just run path2chi() on the paths for which we want to recalculate \(\chi\). Note that we specify the paramgroup to path2chi() here.

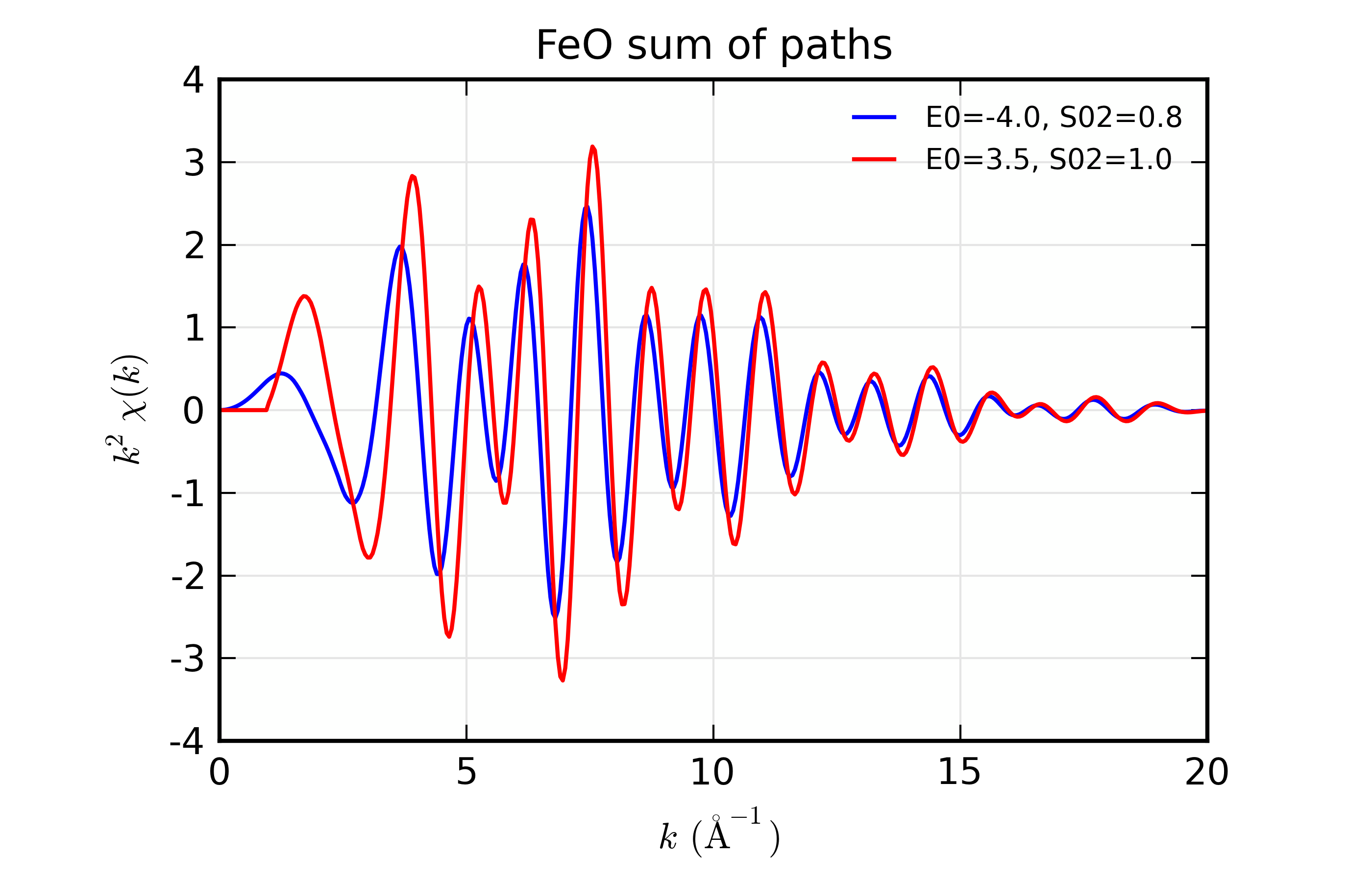
Figure 14.7.9.1 Results for making 2 different sums of paths using parameterized Path Parameters

The resulting plot shows the effect of changing \(E_0\) and \(S_0^2\) for a sum of paths. The same result could be shown by just setting the path parameters to the appropriate numerical values, but the use of parameters makes this somewhat more general. As we will see in the next section, the use of parameters also allows us to easily refine their values in a fit of XAFS data to such a sum of paths.

Footnotes

[1]

There have been several names used for “Free version of Feff Version 8.5 for EXAFS only”, including Feff8l, Feff8lite, Feff85exafs. These all refer to the same project and code, which is based on but distinct from the Feff 8 and 9 from the University of Washington group in that the free version can calculate only EXAFS.